¿Cómo averiguar el gasoil que queda en el depósito?

El pasado lunes, en una reunión de la comunidad de propietarios, alguien planteó un problema: la construcción de una cala que sirviese para saber en cada momento la cantidad de gasoil que queda en el depósito comunitario. Dicho depósito se encuentra acostado bajo la rampa de acceso al garaje. Cuando hablo de acostado me refiero a que, con su forma cilíndrica, descansa sobre la cara lateral, no sobre una de las bases.

En la parte superior de esa cara lateral tiene un orificio por el que se introduce el gasoil. Este orificio lleva un tapón (el de llenado), al que se tiene acceso desde la rampa del garaje. La cala habría que introducirla verticalmente, quitando la tapadera y el tapón de acceso, hasta que tocase el fondo. Estaría construida en acero oscuro (valen otros materiales). Al sacarla del depósito quedaría impregnada en gasoil hasta una determinada altura, lo que serviría para averiguar el gasoil que queda en el depósito.

La cala deberá llevar unas marcas que indiquen en cada circunstancia el volumen de gasoil. Esas marcas habrá que hacerlas en función de la altura (radio) del depósito. Sabemos que dicho radio es de 1 metro y que la altura del depósito (altura del cilindro) es de 3 metros.

¿Qué proceso (cálculos) debemos seguir para hacer las marcas en la cala? (Explica, por ejemplo, el volumen que corresponde a 10 cm de altura).

_______________________

Solución

Los que no sean capaces de resolver el problema o quieran comprobar si su solución es válida, pueden leer lo que viene a continuación:

Para calcular el volumen del depósito cilíndrico habrá que multiplicar el área de la base (círculo) por la altura. Si queremos calcular el volumen de líquido que hay en el depósito cuando la cala marca 10 cm, habrá que considerar en la base del cilindro un segmento circular y multiplicar su área por la altura (3 metros).

¿Cómo se calcula el área de un segmento circular?

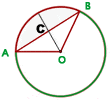
Sabemos que un segmento circular es la porción de superficie plana limitada por una cuerda y un sector circular. En la figura sería la porción limitada entre la cuerda AB y el sector circular AOB. Habría que restar del área del sector el área del triángulo. Haremos lo siguiente:

1. Ángulo AOC: Sabemos que AC mide 0,90 m ya que la altura desde el fondo del depósito es de 10 cm = 0,10 m. Así que el ángulo será el arco coseno de 0,90 = 25,84º.
2. Ángulo AOB: Es el doble del ángulo AOC = 51,68º.
3. Segmento AC: Aplicando el teorema de Pitágoras, sería el valor de la raíz cuadrada del cuadrado de la hipotenusa (1) menos el cuadrado del cateto OC (0,9) = 0,44 m.
4. Base del triángulo: Valor de AC multiplicado por dos = 0,88 m.
5. Área del triángulo: Base por altura dividido entre dos = 0,88 x 0,90 / 2 = 0,396 metros cuadrados.
6. Área del sector circular: Producto de pi (3,14) por el radio del círculo elevado al cuadrado y por el ángulo del sector, dividido entre 360º = 0,45 metros cuadrados.
7. Área del segmento circular: Área del sector circular – Área del triángulo = 0,45 – 0,396 = 0,054 metros cuadrados.

¿Cómo se calcula el volumen del cilindro que corresponde a la altura de los 10 cm?

• Habrá que multiplicar el área del segmento circular por la altura del cilindro = 0,054 x 3 = 0,162 metros cúbicos.

De forma similar se puede calcular el volumen correspondiente a 20, 30, 40… cm hasta 100 cm, el radio del cilindro. En la cala, al lado de cada medida habrá que indicar el volumen correspondiente.