Un conocido terrateniente, del que no vamos a decir su nombre, quiso recompensar a sus dos hijos con dos porciones de terreno de su propiedad. Había, eso si, una condición: las dos deberían ser del mismo perímetro.

Aurelio, el mayor, escogió una superficie en forma de triángulo equilátero. El área de su elección fue de 2.000 metros cuadrados.
Remigio quiso un terreno de forma de hexágono regular. ¿Cuál era el área de esta segunda superficie?
________________
Solución
Los que no sean capaces de resolver el problema o quieran comprobar si su solución es válida, pueden leer lo que viene a continuación:
Vemos que AB es igual a dos veces CD. De esta forma los perímetros del triángulo y del hexágono son iguales.
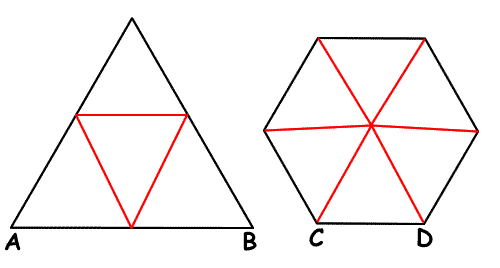
Vemos también que el terreno triangular se puede dividir en 4 triángulos equiláteros iguales y el hexagonal en 6 del mismo tamaño. Por tanto el área del hexágono será 6/4 = 3/2 de la del triángulo.
Así que, el terreno elegido por Remigio, tiene un área de 3.000 metros cuadrados.





