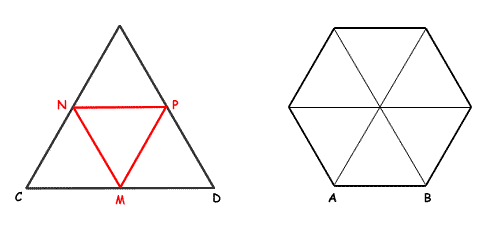
Tenemos un triángulo equilátero de lado CD y un hexágono regular de lado AB.
Las dos figuras anteriores tienen perímetros iguales. El lado del triángulo es doble del lado del hexágono. Es decir, CD = 2AB.
Si unimos los puntos medios de los lados del triángulo (M, N y P), obtenemos cuatro triángulos equiláteros iguales. Vemos también que el hexágono se puede dividir en seis triángulos equiláteros, también iguales a las divisiones del triángulo grande.
Se deduce, por tanto, que la superficie del hexágono es los 6/4 = 3/2 de la del triángulo. Así la superficie del hexágono será los 3/2 de 20, es decir, 30 iterus.



