A Remigio no le costó gran esfuerzo pintar el anillo sobre aquel suelo áspero y absorbente. Su jefe se lo había advertido: «Fíjate en la pintura que gastas».
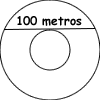
Remigio trabajaba como pintor a sueldo porque, según él, no sabía hacer otra cosa, a pesar de su gran afición a las matemáticas. Sobre un trozo de papel dibujó dos círculos concéntricos y trazó la tangente al círculo interior en uno de sus puntos.
El segmento determinado sobre el círculo exterior era de 100 metros.
El jefe se enfadó muchísimo. Pero Remigio le propuso una rápida solución para averiguar la superficie de la corona circular. ¿Cuál fue ésta?
_______________________
Solución
Los que no sean capaces de resolver el problema o quieran comprobar si su solución es válida, pueden leer lo que viene a continuación:
Si reducimos el circulo interior hasta que su radio sea cero, la cuerda trazada se convertirá en el diámetro del círculo exterior.
El área de este nuevo círculo coincidirá con el área de la corona inicial:
3,14×50^2 = 7.854 metros cuadrados




